Mathematician, physicist, religious philosopher and wordsmith: By any standard, Blaise Pascal exemplified the term Renaissance man.
- It's no secret that Roulette is all about odds, house edges, and statistics. So it should come as no surprise that the Roulette wheel was actually invented by Blaise Pascal, a French physicist, inventor, and mathematician. But Pascal wasn't trying to invent a casino game. In 1655, Pascal tried to invent a perpetual motion machine.
- Jul 04, 2016 Pascal revolutionized mathematics in his early years, then moved on to science where he dabbled in gambling again by inventing the Roulette wheel while exploring perpetual motion. He then mostly gave up on math and science to become one of history's most famous philosophers in the ripe old age of twenty-something (26 if the above video is.
Who Invented Roulette? Back in 1655, the French inventor, physicist, and mathematician named was working on a perpetual motion machine. If you forgot your Science-to-English dictionary, it's basically a machine that would continue to run without having to draw any outside energy. If you've studied physics, you know that's not.
Born on June 19, 1623, in Clermont-Ferrand, France, Pascal established himself in his early teens as a self-taught mathematical prodigy [source: Britannica; 'Prodigy']. At the tender age of 16, he dreamed up Pascal's theorem. According to the theorem, if you draw any hexagon inside any conic section (the curve that occurs when a plane intersects a cone) and then extend the lines of opposite sides, they will meet in three points lying on the same line.
Advertisement
Advertisement
Switching gears, Pascal built one of the first digital calculators in 1642 to aid his father, a mathematician and tax collector, humbly dubbing it the pascaline. The pascaline used gears and pins to perform integer addition. Through a few simple mathematical tricks, a person could also use it to subtract, multiply and divide. Different versions could handle five-, six- and eight-digit numbers. The real trick, though, lay in tackling the nondecimal French monetary denominations, in which 20 sols equaled a livre and 12 deniers made a sol.
As a spinoff of his work on perpetual motion, which he explored in his efforts to improve the pascaline, Pascal also invented the core technology of the roulette machine [source: MIT].
Grade-schoolers still learn Pascal's triangle, a three-sided arrangement of integers such that every number equals the sum of two diagonal numbers above it, as the accompanying illustration demonstrates. Pascal didn't invent the configuration (Chinese and Persian mathematicians used it more than 500 years earlier). However, he found novel uses for it, including calculating probabilities.
In 1654, Pascal, now a worldly 31, brought his knack for formalization and analysis to bear once again as he worked with Pierre de Fermat to establish the calculus of probabilities. While corresponding to solve a gambling puzzle, the two men hit upon the idea of equally probable outcomes, a fundamental concept that had eluded other analysts. A coin flip landing heads or tails, or a single die roll coming up any number from 1-6, are examples of equally probable outcomes. Pascal codified their findings into a general rule for calculating probability, using his handy triangle to simplify the calculations [source: Fermat and Pascal].
Like any Renaissance man worth his salt, Pascal's talents weren't limited to one subject area. Up next, we'll see how his contributions to physics, metaphysics and letters also would reverberate for years to come.
Advertisement

As Pascal grew older, he began delving increasingly into the physical sciences and Christian philosophy.
Around 1646, he began a series of atmospheric pressure experiments to test the theories of Galileo and Galileo's student Evangelista Torricelli (the Italian physicist who identified the principle governing barometers). Cobbling together his own mercury barometers, Pascal undertook expanded versions of his predecessors' experiments, producing findings that helped lay the foundations for hydrodynamics and hydrostatics [source: Britannica; 'Blaise Pascal']. Eventually, he even got a unit of pressure measurement named after him, the Pascal.
Advertisement
Advertisement
Pascal's pressure experiments also inspired him to invent the syringe and the hydraulic press. The latter derived from an observation that we now know as Pascal's Law: External pressure exerted on a confined liquid propagates undiminished through the liquid in all directions no matter where the pressure is applied.
Hydraulic presses use this principle to create mechanical advantage: When a small amount of force pushes a small piston a long distance into an incompressible fluid (like water, oil or hydraulic fluid), a larger and heavier piston on the other end of the fluid system will move upward a short distance. Think of it as liquid leverage. Just as a lever allows you to lift a heavier weight than you normally could, the force multiplication described by Pascal's Law explains how hydraulic lifts elevate cars and how hydraulic brakes apply enough force to stop a several-hundred-ton airplane.
Brilliant as his technical inventions and physical research were, Pascal gained perhaps more fame for his far-reaching contributions to philosophy and Christian thought. His best-known philosophical invention was Pascal's Wager, the argument that pragmatism demands living your life as if God exists, because you will lose little if God is a myth but stand to gain immeasurably (eternal life) if God is real [source: Honderich; 'Pascal's Wager'].
Now a religious philosopher and Christian apologist, Pascal argued for the Christian faith and for God's existence using psychology and history, instead of relying on more typical metaphysical analysis [source: Honderich; 'Blaise Pascal']. He set out much of his argument in his unfinished work of Christian apologetics, Apologie de la religion chrétienne, which scholars later collected with other notes in a work known as Pensées (Thoughts) [source: Britannica; 'Blaise Pascal'].
Pascal's inventiveness extended to literature as well. His work Provincales -- an attack on Jesuits in defense of Antoine Arnauld, a defender of Jansenism on trial at the time -- remains popular to this day. Nicolas Boileau, the founder of French literary criticism, considered Pascal's writings to mark the beginning of modern French prose [source: Britannica; 'Blaise Pascal'].
Like Archimedes or Galileo, Pascal was a true polymath, the product of a disciplined, curious and analytical mind.
Advertisement
Related Articles
Sources
- American Heritage Science Dictionary. 'Pascal's Law.' 2005. Houghton Mifflin Company.http://www.thefreedictionary.com/Pascal%27s+law
- Encyclopedia Britannica Online. 'Blaise Pascal.' (March 19, 2011)http://www.britannica.com/EBchecked/topic/445406/Blaise-Pascal
- Encyclopedia Britannica Online. 'Prodigy.' 2011. (March 19, 2011)http://www.britannica.com/EBchecked/topic/477899/prodigy
- Fermat, Pierre de and Blaise Pascal. 'Fermat and Pascal on Probability.' (March 21, 2011)http://www.york.ac.uk/depts/maths/histstat/pascal.pdf
- Hazewinkel, Michiel. 'Pascal's Theorem.' Encyclopedia of Mathematics. 2002.
- Hazewinkel, Michiel. 'Pascal's Triangle.' Encyclopedia of Mathematics. 2002.
- Honderich, Ted. 'Pascal's Wager.' The Oxford Guide to Philosophy. 2005.
- Honderich, Ted. 'Blaise Pascal.' The Oxford Guide to Philosophy. 2005.
- Massachusetts Institute of Technology School of Engineering. 'Mechanical Calculator.' May 2003. (March 20, 2011)http://web.mit.edu/invent/iow/pascal.html
Unless you master pascal triangle, it is unlikely that you can be a good gambler. You must master pascal triangle if you want to be a good gambler. Pascal triangle gives you the structure to win yet stay away from gambling tilt.
Pascal Triangle is a marvel that develops from a very basic simple formula. Pascal triangle became famous because of many of its patterns.
Before you start looking at patterns, just learn how to write your own pascal triangle. This is for those who do not have flare in mathematics.
Pascal Triangle is formed by starting with an apex of 1. The first row is counted as row zero. Every number below in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero.
Now, you may take a look at patterns within the pascal triangle.
PATTERN 1
General patterns found within Pascal Triangle
Heads or Tails, Even or Odd, Black or Red, Big or Small, Banker or Player.
Pascal Triangle can show you how many ways heads and tails can combine. You can then use the pascal triangle to see the odds or probability of any combination.
For example, if you toss a coin three times, there is only one combination that will give you three heads (HHH), but there are three combinations that will give two heads and one tail (HHT, HTH, THH), also three that give one head and two tails (HTT, THT, TTH) and one for all Tails (TTT). This is the pattern '1,3,3,1' in Pascal Triangle in row 3.
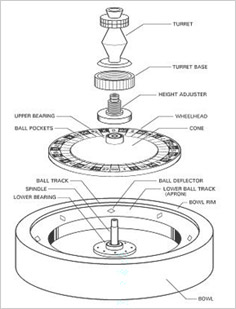
Blaise Pascal Roulette Machine
You are assuming that the orders are the same. In other words, (HHT, HTH, THH), (HTH, HHT, THH) and (HTH, THH, HHT) are the same. Bear in mind that in actual gambling they are not the same. You have to make adjustment for that.
Example: What is the probability of getting exactly two heads with 4 coin tosses?
There are 1+4+6+4+1 = 16 (or 2 to the power 4=16) possible results, and 6 of them give exactly two heads. So the probability is 6/16, or 37.5%. Why 37.5%. Why not 50% since two heads out of four. Try to figure it out yourself. (Hint: The rules here is different from the rules in gambling. Here, you win only when the outcome is two heads. You lose when the outcome is one head, three heads and four heads.)
You have seen that Pascal triangle is constructed very simply—each number in the triangle is the sum of the two numbers immediately above it. It is also assumed that you now know how to construct pascal triangle with ease.
Pascal triangle is very useful for finding the probability of events where there are only two possible outcomes. This includes tossing a coin where the outcomes are either head or tail. In mini-dice and Tai-Sai, you have big or small. In roulette, you have black or red, big or small, even or odd. In baccarat, you have banker or player.
For example, if you bet three times in baccarat, there are eight (2x2x2 or 2 to the power 3) possibilities:
BBB BBP BPB PBB PPB PBP BPP PPP
If you look at Row 3 of the triangle, you can see the numbers 1,3,3,1. This tells you that there is only one way of obtaining all BANKERS or all PLAYERS, but three ways of obtaining two BANKERS and one PLAYERS, or two PLAYERS and one BANKER. Translated to probabilities, the chances of the possible outcomes are:
3B—1/8 (one in eight) 2B1P—3/8 2P1B—3/8 3P—1/8 (one in eight)
Refer to Pascal triangle again, and take a look at row 4. Looking at Row 4, you can see that for a set of four bets, one PLAYER and three BANKER is four times as common as having FOUR BANKER and no PLAYER, while a set of four bets with two BANKERS and two PLAYERS are six times as common. There is only one chance in 16 (2 to the power 4) of a set of four having all BANKERS or all PLAYERS. And so on.
COMBINATIONS
The pascal triangle also shows you how many combinations of objects are possible.
Example: You placed 16 bets. How many times would you win only three bets and lost 13 bets? This is a typical gambling scenario.
Answer: go down to row 16 (the top row is 0), and then along 3 places and the value there is your answer, 560.


Pascal's Roulette Machine
PATTERN 2
Patterns found within Diagonals

As Pascal grew older, he began delving increasingly into the physical sciences and Christian philosophy.
Around 1646, he began a series of atmospheric pressure experiments to test the theories of Galileo and Galileo's student Evangelista Torricelli (the Italian physicist who identified the principle governing barometers). Cobbling together his own mercury barometers, Pascal undertook expanded versions of his predecessors' experiments, producing findings that helped lay the foundations for hydrodynamics and hydrostatics [source: Britannica; 'Blaise Pascal']. Eventually, he even got a unit of pressure measurement named after him, the Pascal.
Advertisement
Advertisement
Pascal's pressure experiments also inspired him to invent the syringe and the hydraulic press. The latter derived from an observation that we now know as Pascal's Law: External pressure exerted on a confined liquid propagates undiminished through the liquid in all directions no matter where the pressure is applied.
Hydraulic presses use this principle to create mechanical advantage: When a small amount of force pushes a small piston a long distance into an incompressible fluid (like water, oil or hydraulic fluid), a larger and heavier piston on the other end of the fluid system will move upward a short distance. Think of it as liquid leverage. Just as a lever allows you to lift a heavier weight than you normally could, the force multiplication described by Pascal's Law explains how hydraulic lifts elevate cars and how hydraulic brakes apply enough force to stop a several-hundred-ton airplane.
Brilliant as his technical inventions and physical research were, Pascal gained perhaps more fame for his far-reaching contributions to philosophy and Christian thought. His best-known philosophical invention was Pascal's Wager, the argument that pragmatism demands living your life as if God exists, because you will lose little if God is a myth but stand to gain immeasurably (eternal life) if God is real [source: Honderich; 'Pascal's Wager'].
Now a religious philosopher and Christian apologist, Pascal argued for the Christian faith and for God's existence using psychology and history, instead of relying on more typical metaphysical analysis [source: Honderich; 'Blaise Pascal']. He set out much of his argument in his unfinished work of Christian apologetics, Apologie de la religion chrétienne, which scholars later collected with other notes in a work known as Pensées (Thoughts) [source: Britannica; 'Blaise Pascal'].
Pascal's inventiveness extended to literature as well. His work Provincales -- an attack on Jesuits in defense of Antoine Arnauld, a defender of Jansenism on trial at the time -- remains popular to this day. Nicolas Boileau, the founder of French literary criticism, considered Pascal's writings to mark the beginning of modern French prose [source: Britannica; 'Blaise Pascal'].
Like Archimedes or Galileo, Pascal was a true polymath, the product of a disciplined, curious and analytical mind.
Advertisement
Related Articles
Sources
- American Heritage Science Dictionary. 'Pascal's Law.' 2005. Houghton Mifflin Company.http://www.thefreedictionary.com/Pascal%27s+law
- Encyclopedia Britannica Online. 'Blaise Pascal.' (March 19, 2011)http://www.britannica.com/EBchecked/topic/445406/Blaise-Pascal
- Encyclopedia Britannica Online. 'Prodigy.' 2011. (March 19, 2011)http://www.britannica.com/EBchecked/topic/477899/prodigy
- Fermat, Pierre de and Blaise Pascal. 'Fermat and Pascal on Probability.' (March 21, 2011)http://www.york.ac.uk/depts/maths/histstat/pascal.pdf
- Hazewinkel, Michiel. 'Pascal's Theorem.' Encyclopedia of Mathematics. 2002.
- Hazewinkel, Michiel. 'Pascal's Triangle.' Encyclopedia of Mathematics. 2002.
- Honderich, Ted. 'Pascal's Wager.' The Oxford Guide to Philosophy. 2005.
- Honderich, Ted. 'Blaise Pascal.' The Oxford Guide to Philosophy. 2005.
- Massachusetts Institute of Technology School of Engineering. 'Mechanical Calculator.' May 2003. (March 20, 2011)http://web.mit.edu/invent/iow/pascal.html
Unless you master pascal triangle, it is unlikely that you can be a good gambler. You must master pascal triangle if you want to be a good gambler. Pascal triangle gives you the structure to win yet stay away from gambling tilt.
Pascal Triangle is a marvel that develops from a very basic simple formula. Pascal triangle became famous because of many of its patterns.
Before you start looking at patterns, just learn how to write your own pascal triangle. This is for those who do not have flare in mathematics.
Pascal Triangle is formed by starting with an apex of 1. The first row is counted as row zero. Every number below in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero.
Now, you may take a look at patterns within the pascal triangle.
PATTERN 1
General patterns found within Pascal Triangle
Heads or Tails, Even or Odd, Black or Red, Big or Small, Banker or Player.
Pascal Triangle can show you how many ways heads and tails can combine. You can then use the pascal triangle to see the odds or probability of any combination.
For example, if you toss a coin three times, there is only one combination that will give you three heads (HHH), but there are three combinations that will give two heads and one tail (HHT, HTH, THH), also three that give one head and two tails (HTT, THT, TTH) and one for all Tails (TTT). This is the pattern '1,3,3,1' in Pascal Triangle in row 3.
Blaise Pascal Roulette Machine
You are assuming that the orders are the same. In other words, (HHT, HTH, THH), (HTH, HHT, THH) and (HTH, THH, HHT) are the same. Bear in mind that in actual gambling they are not the same. You have to make adjustment for that.
Example: What is the probability of getting exactly two heads with 4 coin tosses?
There are 1+4+6+4+1 = 16 (or 2 to the power 4=16) possible results, and 6 of them give exactly two heads. So the probability is 6/16, or 37.5%. Why 37.5%. Why not 50% since two heads out of four. Try to figure it out yourself. (Hint: The rules here is different from the rules in gambling. Here, you win only when the outcome is two heads. You lose when the outcome is one head, three heads and four heads.)
You have seen that Pascal triangle is constructed very simply—each number in the triangle is the sum of the two numbers immediately above it. It is also assumed that you now know how to construct pascal triangle with ease.
Pascal triangle is very useful for finding the probability of events where there are only two possible outcomes. This includes tossing a coin where the outcomes are either head or tail. In mini-dice and Tai-Sai, you have big or small. In roulette, you have black or red, big or small, even or odd. In baccarat, you have banker or player.
For example, if you bet three times in baccarat, there are eight (2x2x2 or 2 to the power 3) possibilities:
BBB BBP BPB PBB PPB PBP BPP PPP
If you look at Row 3 of the triangle, you can see the numbers 1,3,3,1. This tells you that there is only one way of obtaining all BANKERS or all PLAYERS, but three ways of obtaining two BANKERS and one PLAYERS, or two PLAYERS and one BANKER. Translated to probabilities, the chances of the possible outcomes are:
3B—1/8 (one in eight) 2B1P—3/8 2P1B—3/8 3P—1/8 (one in eight)
Refer to Pascal triangle again, and take a look at row 4. Looking at Row 4, you can see that for a set of four bets, one PLAYER and three BANKER is four times as common as having FOUR BANKER and no PLAYER, while a set of four bets with two BANKERS and two PLAYERS are six times as common. There is only one chance in 16 (2 to the power 4) of a set of four having all BANKERS or all PLAYERS. And so on.
COMBINATIONS
The pascal triangle also shows you how many combinations of objects are possible.
Example: You placed 16 bets. How many times would you win only three bets and lost 13 bets? This is a typical gambling scenario.
Answer: go down to row 16 (the top row is 0), and then along 3 places and the value there is your answer, 560.
Pascal's Roulette Machine
PATTERN 2
Patterns found within Diagonals
The first diagonal is, of course, just '1's, and the next diagonal has the Counting Numbers (1,2,3, 4,5,6,7,etc).
Experience Call of Duty: the world's best-selling video game franchise. Discover the latest updates to this first person shooter series all in one place. COD Online Welcome to the U.S. Department of Education's Common Origination and Disbursement (COD) web site. Financial Aid Administrators, Servicers, or other officials can use this site to perform a. Experience the thrill of Call of Duty on the go. Play as iconic characters in battle royale and multiplayer in our best fps free mobile game. Download free now. Play now Call Of Duty Online online on Kiz10.com. Have fun playing Call Of Duty Online One of the best Action Game on Kiz10.com. Call of Duty Online (Now called Army Force Strike) is a massive multiplayer online first person shooter on the Call of Duty franchise. The game features a beautiful 3D graphics while maintaining a smooth gameplay which is a big plus for any competitive FPS games. Call of Duty Online.
The third diagonal has the triangular numbers 1,3,6,10,15,21
The fourth diagonal has the tetrahedral numbers 1,4,10,20,35.
The fifth diagonal has the pentagonal numbers.
The sixth diagonal has the hexagonal numbers.
The Fibonacci Series is also found within the diagonals in the Pascal's Triangle.
The numbers on diagonals of the triangle add to the Fibonacci series, as shown below.
I will discuss the significance of fibonacci numbers in gambling, nature and life in a separate post.
PATTERN 3
Patterns found within horizontals
Notice that each horizontal rows add up to powers of 2 (i.e., 1, 2, 4, 8, 16, etc).
The horizontal rows represent powers of 11 (1, 11, 121, 1331, etc).
Adding any two successive numbers in the diagonal 1-3-6-10-15-21-28… results in a perfect square (1, 4, 9, 16, etc).
PATTERN 4
Pascal Haas Roulette
When the first number to the right of the 1 in any row is a prime number, all numbers in that row are divisible by that prime number. Try it yourself to appreciate.
PATTERN 5
Pattern 5 is combinatoric mathematics. Combinatorics is the science that studies the numbers of different combinations, which are groupings of numbers. Combinatorics is often part of the study of probability and statistics.
Fractal is a term coined by Benoit Mandelbrot in 1975, referring to objects built using recursion, where some aspect of the limiting object is infinite and another is finite, and where at any iteration, some piece of the object is a scaled down version of the previous iteration. A good example of geometric fractal is the Sierpinski Triangle which is an ever repeating pattern of triangles.
PATTERN 6
Pattern 6 is the CATALAN NUMBERS
The Catalan Numbers are a sequence of numbers which show up in many contexts. They were discovered by Leonhard Euler when he was attempting to find a general formula to express the number of ways to divide a polygon with N sides into triangles using non-intersecting diagonals . The Catalan Numbers' correspondence to the division of polygons is shown below:
You can see in next Pascal Triangle that each Catalan number is the sum of specific Pascal numbers.(© Dirk Laureyssens, 2004)
I will discuss the significance of catalan numbers in computer science and programming in a separate post.
Amazon.com Widgets
Social Bookmarking
